Historia de la Geometría

Este es el primer texto de la historia de la geometría, consiste en una recopilación de diferentes textos y diferentes estructuras de recopilación.

Hasta han llegado a decir que "el origen de la geometría coincide con el origen de la humanidad, por ejemplo, la abstracción del pensamiento mágico representa el primer acercamiento a la geometría".   

Grandes físicos, filósofos y matemáticos

Arquímedes de Siracusa 

(287 a.c.- 212 a.c.)

Matemático, físico e inventor.

Aunque no se conocen muchos detalles de su vida, fue uno de los científicos y matemáticos mas importantes de la antigüedad clásica. 

Aportó a esta ciencia el "Principio de Arquímedes" que explica el empuje que recibe un cuerpo al ser sumergido en un líquido. También está su principio de la Palanca y su experimento de espejos que reflejan la luz.

Isaaz Newton

( 4 de marzo 1643 - 31 de marzo 1727 )

Físico, matemático e inventor.

autor de los philosophiae naturalis principia mathematica, más conocidos como los Principia, donde describió la ley de gravitación universal y estableció las bases de la mecánica clásica mediante las leyes que llevan su nombre. No esta de mas decir que hizo trabajos sobre la luz y óptica.

Newton también fue el primero en demostrar que las leyes naturales que gobiernan el movimiento en la tierra y las que gobiernan el movimiento de los cuerpos celestes son las mismas.

Blaise Pascal

( 19 de junio 1623 - 19 de agosto 1662 )

Matemático, físico y filósofo

Sus contribuciones a las matemáticas y las ciencias naturales incluyen el diseño y construcción de calculadoras mecánicas, aportes a la teoría de la probabilidad, investigaciones sobre los fluidos y la aclaración de conceptos tales como la presión y el vació. Después de una experiencia religiosa profunda en 1654, Pascal abandonó las matemáticas y la física para dedicarse a la filosofía y a la teología.

Es conocido por su principio de Pascal, que indica que un fluido mantendrá la misma presión en todas sus partes. Gracias a su principio usamos la prensa hidráulica para levantar objetos pesados sin mucho esfuerzo.

Estos fueron también algunos físicos, filósofos y matemáticos:

- Albert Eintein

- Galileo Galilei

- Faraday

- Coulomb

- Lord Kelvin

- Stephen Hawking

- Marie Curie (es mujer)

- Daniel Bernoulli

- Christian Doppler

Definición de Geometría

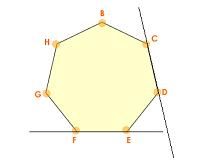
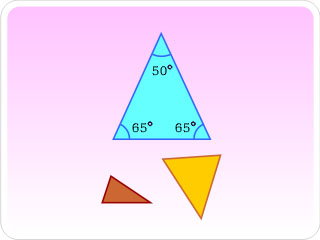
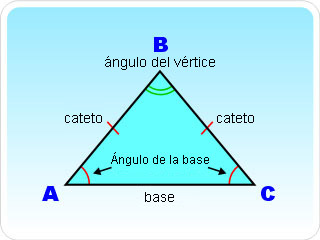
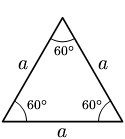
La geometría es una parte de la matematica que trata de estudiar unas idealizaciones del espacio en que vivimos, que son los puntos, las rectas, los planos, y otros elementos conceptuales derivados de ellos, como poligonos o poliedros.

En la practica, la geometría sirve para solucionar problemas concretos en el mundo de lo visible. Entre sus utilidades se encuentran la justificación teorica de muchos instrumentos: compás, teodolito, pantógrafo, sistema de posicionamiento global. También es la que nos permite medir areas y volumenes, es útil en la preparación de diseños, e incluso en la fabricación de artesanías.

La geometria clásica o axiomática es una matemática en la cuál los objetos, en vez de ser números, son puntos, rectas, planos y otras figuras definidas en función de estas.

Ángulos y clases de ángulos

Un ángulo es la parte del plano comprendida entre dos semirrectas que tienen el mismo punto de origen o vértice. Suelen medirse en unidades tales como el radián, el grado sexagesimal o elgrado centesimal.

Pueden estar definidos sobre superficies planas ( trigonometría plana) o curvas (trigonometría esférica).

                  
Clasificación de ángulos según su medida:

Agudo < 90°	Recto = 90°	Obtuso>90°
Convexo < 180°	Llano = 180°	Cóncavo > 180°
Nulo = 0º	Completo = 360°
Negativo < 0º	Mayor de 360°

     
Tipos de ángulos según su posición:

Ángulos consecutivos

Ángulos consecutivos son aquellos que tienen el vértice y un lado común.

Ángulos adyacentes

Ángulos adyacentes son aquellos que tienen el vértice y un lado común, y los otros lados situados uno en polongación del otro.

Punto, recta, semirrecta y segmento

Me gustaria aclarar la diferencia entre: Punto, recta, semirrecta y segmento.
Ahí en la imagen se ve una recta, donde se marcan tres puntos: o, A y B. Entonces ¿cómo definimos una recta? Definimos una recta como una sucesión infinita de puntos ordenados.¿cómo definimos una semirrecta? Definimos una semirrecta como la porción de una recta que tiene principio pero no tiene fin. Tal la imagen, el inicio es O, cuando se habla de semirrecta oA, se indica con A la dirección de dicha semirrecta. En esa imagen hay dos semirrectas, su union forma la recta.¿cómo definimos un segmento?Un segmento de recta es una porción de la recta con principio y con fin, es decir sabemos donde empieza y donde termina por donde lo podemos medir.

Mediatriz y bisectriz

Mediatrices de un triángulo

Mediatriz es cada una de las rectas perpendiculares trazadas 
a un lado por su punto medio.

Circuncentro

Es el punto de corte de las tres mediatrices.

Es el centro de una circunferencia circunscrita al   triángulo.

Bisectrices de un triángulo

Bisectriz es cada una de las rectas que divide a un ángulo 
en dos ángulos iguales.

Incentro

Es el punto de corte de las tres bisetrices.

Es el centro de una circunferencia inscrita en el triángulo.

Recta paralela y perpendicular

Rectas paralelas

Dos rectas son paralelas si tienen el mismo vector director o la misma pendiente.

Rectas perpendiculares

Si dos rectas son perpendiculares tienen sus pendientes inversas y cambiadas de signo.

Dos rectas son perpendiculares si sus vectores directores son perpendiculares.

Definición de polígonos

Un polígono es una porción de plano limitada por líneas rectas. Se trata de una figura geométrica que está formada por segmentos consecutivos no alienados, que reciben el nombre de lados.

Existen diversas clasificaciones de los polígonos. Se conoce como polígono simple a aquel en el que dos de sus aristas no consecutivas no se cortan. En elpolígono complejo, en cambio, dos de sus aristas consecutivas sí se cortan.

Tipos de poligonos

Polígonos regulares

los polígonos regulares tiene sus lados y ángulos iguales. los polígonos regulares están inscritos en una circunferencia. 

Polígonos irregulares

los polígonos irregulares no tiene todos sus lados iguales. sus vértices no están inscritos en una circunferencia.

Polígonos inscritos

un polígono esta inscrito en una circunferencia cuando todos sus vértices son puntos de la circunferencia y todos sus lados están incluidos dentro del circulo que esta define.

Polígonos circunscritos

un polígono esta circunscritos en una circunferencias, si sus vértices están situados fuera de la circunferencia, y sus lados son tangentes a la circunferencia.

Polígonos estrellados

un polígono estrellado se construye uniendo los vértices no consecutivos, de un polígono regular convexo, de forma continua. se denotan por N/M, siendo N el numero de vértices del polígono regular convexo y M el saldo entre vértices. N/M ha de ser fracción irreducible.
un polígono N/M es el mismo que el N/(N-M), ya que el polígono que se obtiene uniendo vértices en un sentido y en el contrario es el mismo.


EJEMPLOS: Pentágono regular estrellado

5/2

Heptágonos regulares estrellados

7/2

Nombres de algunos poligonos

Éstos son los nombres de los polígonos de menos de veinte lados:

Número de lados	Nombre del polígono
3	Triángulo
4	Cuadrilátero
5	Pentágono
6	Hexágono
7	Heptágono
8	Octágono
9	Eneágono o Nonágono
10	Decágono
11	Endecágono
12	Dodecágono
13	Triskaidecágono
14	Tetradecágono
15	Pentadecágono
16	Hexadecágono
17	Heptadecágono
18	Octadecágono
19	Eneadecágono

Teorema de Pitagoras

	En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de loscuadrados de los catetos. a2 + b2 = c2
Cada uno de los sumandos, representa el área de un cuadrado de lado, a, b, c. Con lo que la expresión anterior, en términos de áreas se expresa en la forma siguiente:
El área del cuadrado construido sobre la hipotenusa de un triángulo rectángulo, es igual a la suma de las áreas de los cuadrados construidos sobre los catetos.

Definición de triangulo

El triangulo es un polígono de tres lados. 
El triangulo esta determinado por tres segmentos de recta que se denominan lados, o por tres puntos no alineados llamados vértices.


                                           


los lados de un triangulo se describen en minúscula, con las mismas letras de los vértices opuestos. los vértices de un triangulo se describen con letras mayúsculas. los ángulos de un triangulo se describen igual que los vértices. 

Triangulo acutángulo

Un triángulo acutángulo es aquel cuyos ángulos interiores tienen menos de 90 grados (cada uno de ellos).

Un buen ejemplo es el clásico triángulo equilátero, cuyos lados son todos iguales y sus ángulos interiores son de 60 grados. Ojo que esto es sólo un ejemplo, ya que asimismo tienes triángulos acutángulos isósceles (con dos lados de la misma medida) y también escalenos (con todos sus lados diferentes en cuanto a su longitud).

Triangulo rectángulo

se llama triángulo rectángulo a todo triángulo que posee un ángulo recto, es decir, un ángulo de 90-grados. Las relaciones entre los lados de un triángulo rectángulo es la base de la trigonometría. En particular, en un triángulo rectángulo se cumple el teorema de Pitágoras.

Triangulo isosceles

Triángulo en el que al menos dos lados son congruentes. A los lados congruentes se les llama catetos. El ángulo formado por los catetos es el ángulo vértice. Los otros dos ángulos son los ángulos base. La base es el lado opuesto al ángulo vértice.

Triangulo escaleno

 si todos sus lados tienen longitudes diferentes (en un triángulo escaleno no hay dos ángulos que tengan la misma medida).


http://www.youtube.com/watch?v=fr3sngOlkLM

Triangulo equilatero

 

Un triángulo equilátero, es un triángulo con tres lados iguales. En la geometría euclídea tradicional, los triángulos equiláteros también son equiangulares, es decir, los tres ángulos internos también son congruentes entre sí, cada ángulo vale 60°. Un triángulo equilátero es un polígono regular; es un caso especial de triángulo isósceles.

Ejercicios

1. De un triangulo rectángulo ABC, se conocen a = 45m y b = 280m. Resolver 

2. De un triangulo sabemos que: a = 6m, B = 45º y C = 105º. calculas los restantes

solución

1. 

 

sen B = 280/415 = 0.6747     B = arc sen 0.6747 = 42° 25′

C = 90° - 42° 25′ = 47° 35′

c = a cos B   c = 415 · 0.7381 = 306. 31 m

2.